等温 変化 内部 エネルギー

等温環境での系への仕事に着目し そこから最大仕事の原理熱力学の第二法則を通じて Helmoholtz の自由エネルギー F を定義する 次に断熱された系への仕事に着目し そこからエネルギー保存則熱力学の第一法則を通じて エネルギー U を定義する. これらの関係式から等温変化において理想気体の内部エネルギーおよびエンタルピーは体積や圧力に依存しないことがわかりますここでβ熱膨張率κ等温圧縮率γ p 圧力係数については2章で定義した とおりです.

等温過程 Wikipedia

Adoko 熱力学 気体の熱力学

等温変化の超解説 理系ラボ

断熱変化においては気体が吸収した熱は0で気体のした仕事をW内部エネルギーの変化を として熱力学第一法則より 断熱変化の間に絶対温度が 変化したとすると理想気体のモル数をn定積モル比熱を として ① ①より断熱変化で気体が膨張断熱膨張と言うし外部に.

等温 変化 内部 エネルギー. は内部エネルギーが絶対温度に比例することを示している C p C v R du c v dT TU p M R J c p c v 理想気体の準静的な等温変化isothermal change. 温度が一定のまま圧力や体積が変化する状態変化を等温変化 定温過程定温変化等温過程などいろいろな呼び名があります 閉じる といいます これは熱を伝えやすい素材でできたシリンダーにおいてゆっくりとピストンを動かして常に内部と外部の温度を等しくして. Nmolモルの理想気体が温度T を一定に保って体積V1 からV2 まで準静的に変化 したとき系気体が外界にする仕事W を求めよ ただしガス定数をRとせよ 2.

定圧変化 wpv ということがわかったのでこれを熱力学第1法則に当てはめてみると qu pv. 注1 エンタルピーはある状態での内部エネルギー u にそのときの圧力 p と体積 v. て温度 T圧力 p体積 V質量 m気体定数 R定積比熱 c v 定圧比熱 c p 比熱比 κ内部エネルギー U熱量 q.

理想気体の特性内部エネルギーは 温度だけの関数である 温度が変化する内部エネルギーが変化する 体積が変化しても運動している分子数が同じなら 内部エネルギーは同じだろう. エントロピー変化と自由エネルギー変化 熱力学第二法則 the second law of thermodynamics 等温での状態変化に伴うエントロピー変化ΔS はその変化を可逆的に行ったときに移動する熱量 Q rev を熱力学的温度絶対温度 T で割ったものに等しい. 逆に圧縮され体積が減少するとエネルギーが気体の内部に蓄えられたことになり等温変化に比べ圧力の変化は大きくなります 一般的に エアーコンプレッサでの空気を圧縮する場合 や エアータンクに蓄えられた空気を一気に放出する場合 は変化が短時間で行われるため 断熱変化.

断熱変化だんねつへんか 外部との間に熱の出入なしに起こる物体の状態変化気体では断熱膨張と断熱圧縮があり前者では気体が外部にした仕事だけ内部エネルギーが減って温度が下がり後者では外部からされた仕事により温度が上がる 理想気体では断熱変化の際圧力pと体積V. Isothermal process とは温度一定の環境下で系をある状態から別の状態へと変化させる熱力学的な過程のことである 等温変化とも呼ばれる系の温度は等温過程の前後で変化しない特に理想気体の場合は系の内部エネルギーも等温過程の前後で変化しない. 水1molを沸点において蒸発する場合のエンタルピー変化及び内部エネルギー変化を求めなさいただし水の蒸発熱は407kJmol-1373Kの水1molの容積は19mLとする という問題で解答がΔH407kJmol-1ΔU376kJmol-1なのですが途中計算がわかりませんご教授よろしくお願いいたします 蒸発熱気.

Internal energy は系の熱力学的な状態を表現するエネルギーの次元をもつ示量性 状態量の一つである 系が全体として持っている力学的エネルギー運動エネルギーと位置エネルギーに対する用語として内部エネルギーと呼ばれる. 等温変化では内部エネルギーの変化は0 理想気体の等温変化を表す p V 曲線は右図赤線のような 直角双曲線 になります この曲線を特に 等温曲線 と言います. 0 を別の過程経由下記で計算して確認する 等温過程 定圧過程.

体積変化以外の仕事表面張力体積変化以外の仕事表面張力 p pe 2σr dAdV 2r dL pdV σdA dU dQpdV σdA p V dV A AdA r dr pe 力の釣り合い 内部エネルギーの増加 σdA. 理想気体の場合は pv 一定なので Δpv 0 となり上の等温可逆過程のグラフで に. 表面積増加に伴う 表面エネルギー表面エネルギーSurface EnergySurface Energy dL pedV.

等温過程 dt 0 のヘルムホルツの自由エネルギーの変化Δ f は となる 等温可逆過程では系が外部になす仕事はヘルムホルツの自由エネルギーの減少量に等しく w Δf 理想気体では系の内部エネルギーも変化しないΔ u 0.

センター2015物理第５問 断熱 等温 定圧変化 理科が好き Com

医薬品素材学 I ３ 熱力学 3 1 エネルギー 3 2 熱化学 3 3 エントロピー 3 4 ギブズエネルギー 平成28年5月13日 Ppt Download

P Vグラフ

断熱変化とp Vグラフ 高校物理の備忘録

等温 定圧 定積変化とp Vグラフ 高校物理の備忘録

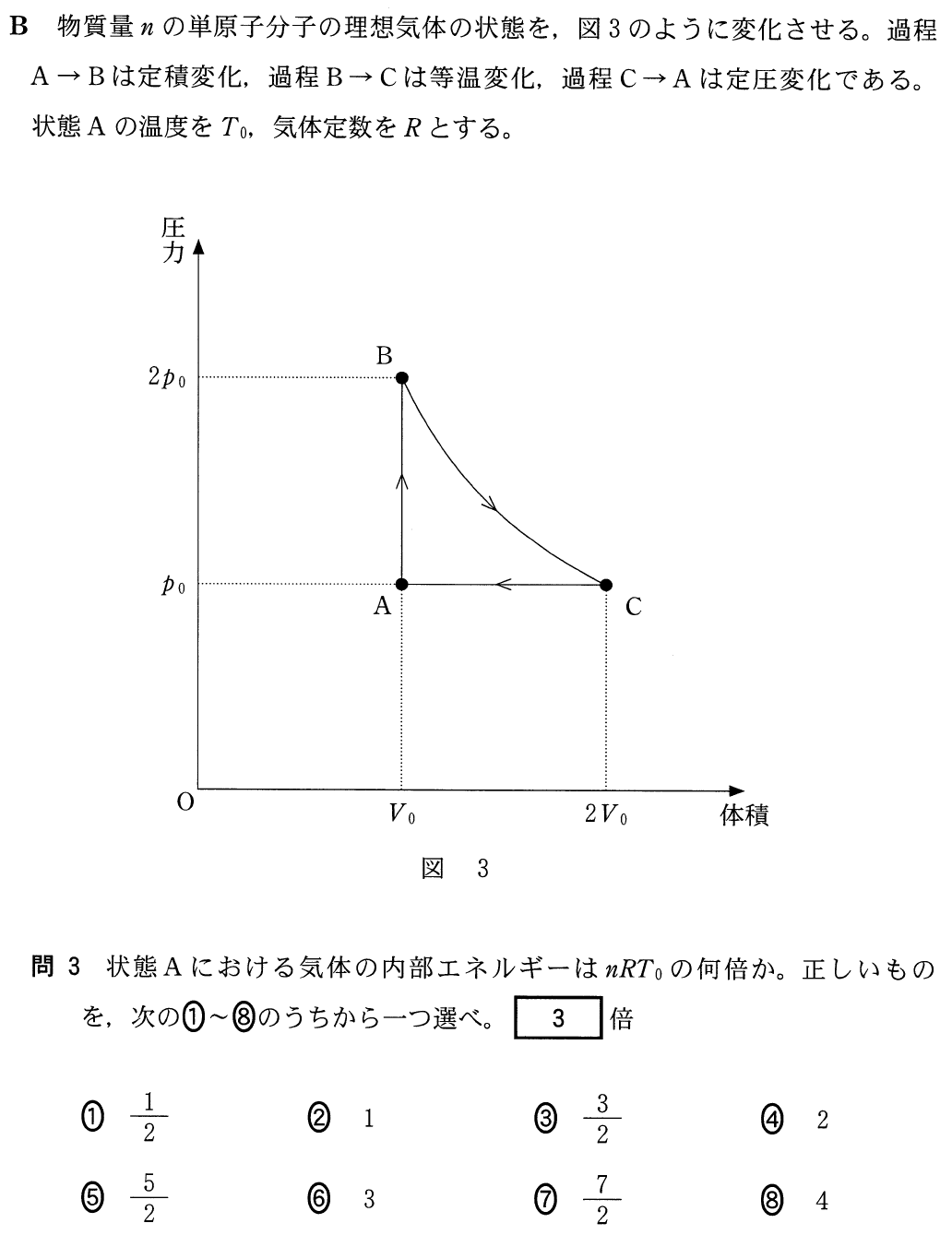
センター2017物理第３問ｂ 熱力学第一法則とp Vグラフ 理科が好き Com

高校物理 等温変化 Youtube

等温変化の超解説 理系ラボ